Columbia Robotics Lab
Abstract
Recent advances in deep reinforcement learning (RL) have demonstrated its potential to learn complex robotic manipulation tasks. However, RL still requires the robot to collect a large amount of real-world experience. To address this problem, recent works have proposed learning from expert demonstrations (LfD), particularly via inverse reinforcement learning (IRL), given its ability to achieve robust performance with only a small number of expert demonstrations. Nevertheless, deploying IRL on real robots is still challenging due to the large number of robot experiences it requires. This paper aims to address this scalability challenge with a robust, sample-efficient, and general meta-IRL algorithm, SQUIRL, that performs a new but related long-horizon task robustly given only a single video demonstration. First, this algorithm bootstraps the learning of a task encoder and a task-conditioned policy using behavioral cloning (BC). It then collects real-robot experiences and bypasses reward learning by directly recovering a Q-function from the combined robot and expert trajectories. Next, this algorithm uses the Q-function to re-evaluate all cumulative experiences collected by the robot to improve the policy quickly. In the end, the policy performs more robustly (90%+ success) than BC on new tasks while requiring no trial-and-errors at test time. Finally, our real-robot and simulated experiments demonstrate our algorithm’s generality across different state spaces, action spaces, and vision-based manipulation tasks, e.g., pick-pour-place and pick-carry-drop.
Detailed Mathematical Derivations
Discriminator’s Objective
To begin, SQUIRL directly recovers a Q function to match the expert’s action conditional distribution:
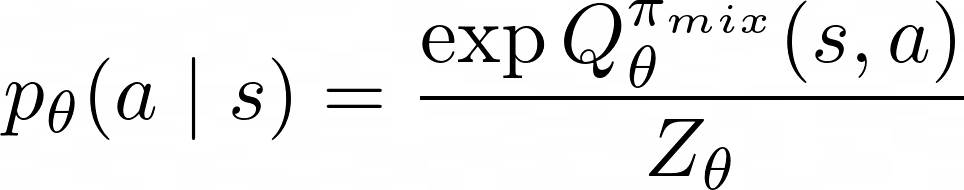
Here, 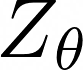 is the partition (normalization) function, an integral over all possible actions given state
is the partition (normalization) function, an integral over all possible actions given state
 that is intractable to compute.
To avoid learning the intractable partition function, we learn the entire entity of
that is intractable to compute.
To avoid learning the intractable partition function, we learn the entire entity of
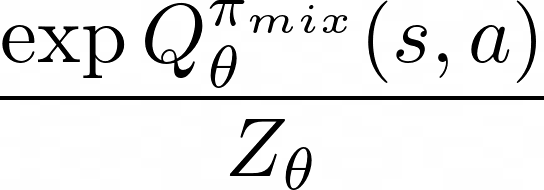 using a single neural network
using a single neural network 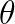 .
To restrict
.
To restrict 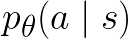 to be a probability lower than 1,
we use a negative ReLU layer activation when computing
to be a probability lower than 1,
we use a negative ReLU layer activation when computing
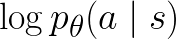 .
The discriminator
.
The discriminator 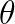 is parameterized in the following form as a binary classifier:
is parameterized in the following form as a binary classifier:
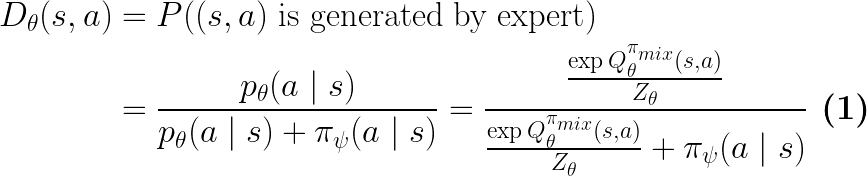
Note that we don’t learn 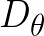 directly,
but learn
directly,
but learn 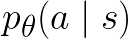 instead.
instead.
Eq.2 in paper
The loss function / optimization objective for the discriminator is Eq.2, not Eq.3. However, below we show that Eq.3 is a part of the Eq.2 objective. To begin, the discriminator’s objective is:
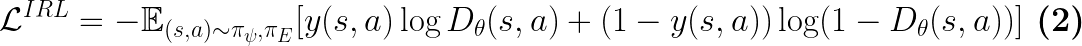
where 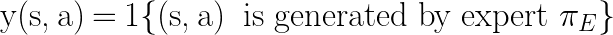
Since we always sample half (50%) of the Q-training data from the policy and the other half from the expert data:
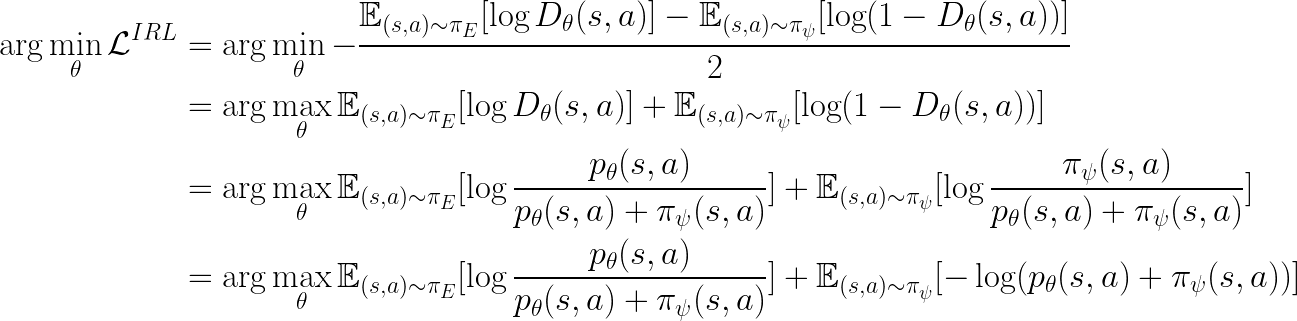
From the first term, we see that:
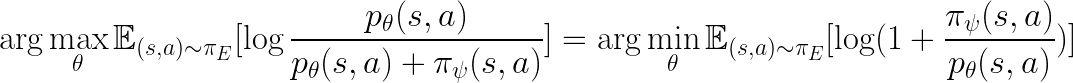
We also see that:
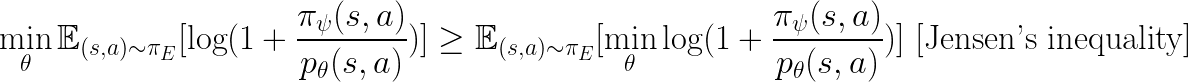
On the other hand:
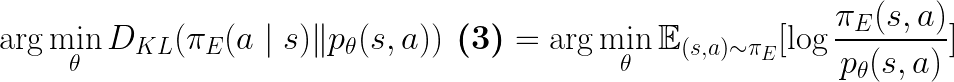
And:
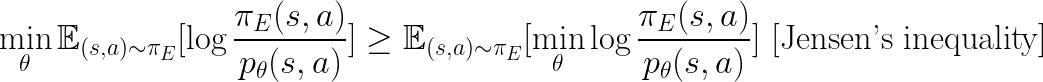
Since:
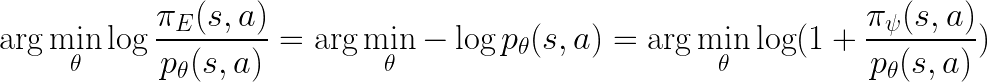
We see that both Eq.2 (part of Eq.2 more precisely) and Eq.3 are trying to minimize the upper bound of the same objective.
Eq.3 in paper
As shown in Eq.3 in the paper, the discriminator is approximating the expert’s conditional action distribution, which is equivalent to recovering a soft Q-function under which the expert is soft Q-optimal:
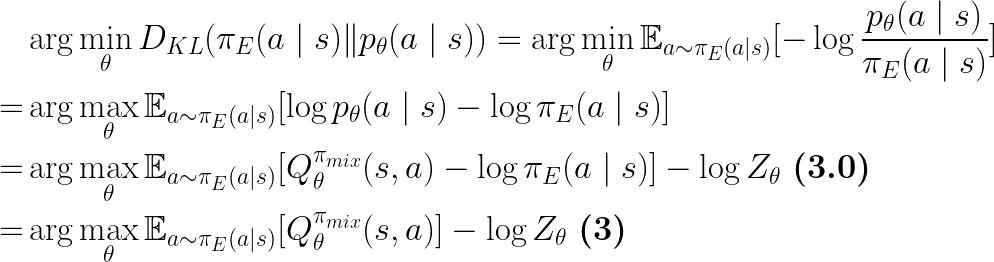
From Eq.3.0, we also see that the discriminator is rationalizing the expert as maximizing both the Q-value and the entropy of its behavior, hence the soft keyword in SQUIRL.
Generator’s Objective
Eq.4 in paper
Under SQUIRL, the policy learning objective (Eq.4 in Paper) is:
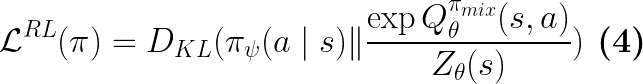
Note that this KL divergence is under the state distribution of the robot-expert mixture policy:
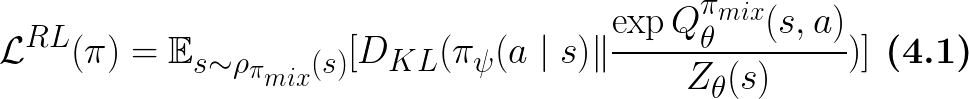
Eq.5 in paper
From Eq.4 and the disciminator’s objective, we see that the policy is essentially matching the predicted expert’s action conditional distribution (Eq.5 in paper):
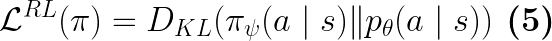
Similar to Eq.4, this KL divergence is also under the state distribution of the robot-expert mixture policy:
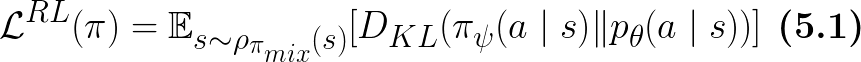
Eq.6 in paper
Therefore, as shown in Eq.6 in the paper, the policy learning objective is also matching the generator’s objective in Generative Adversarial Networks (GANs):
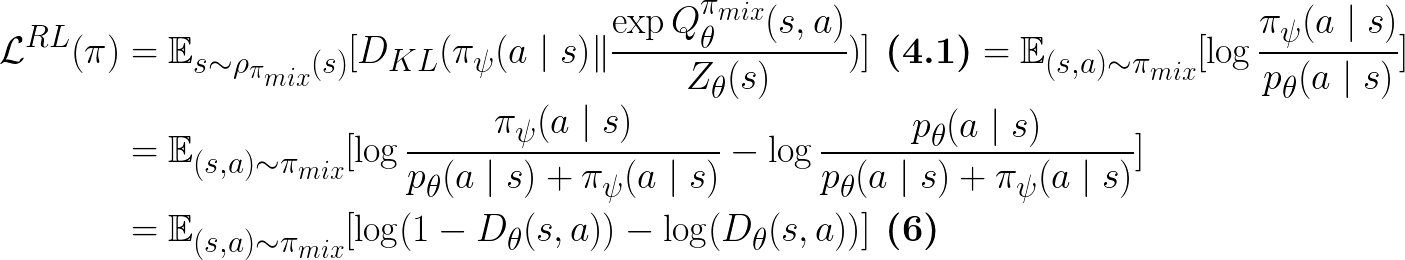
Eq.7 in paper
In addition, since:
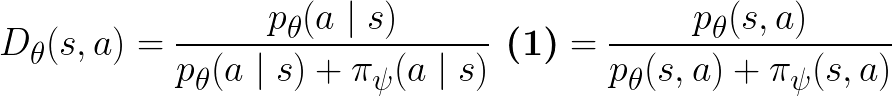
We have:
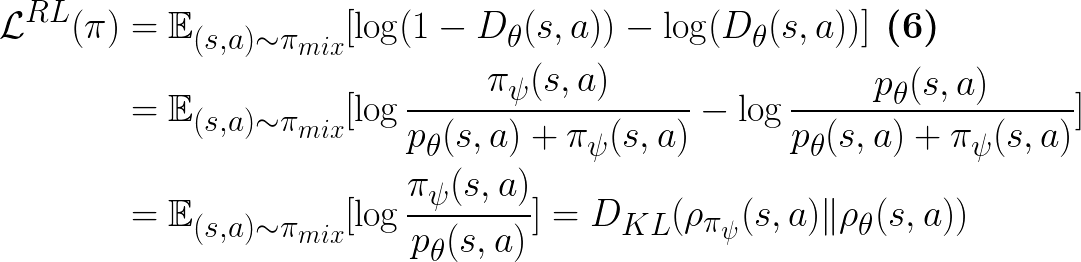
Meanwhile, the discriminator  is matching its Q-function to the log-distribution of the expert's conditional action distribution, i.e., Eq.3.
When the discriminator is optimal:
is matching its Q-function to the log-distribution of the expert's conditional action distribution, i.e., Eq.3.
When the discriminator is optimal:
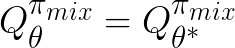 , we see that
, we see that
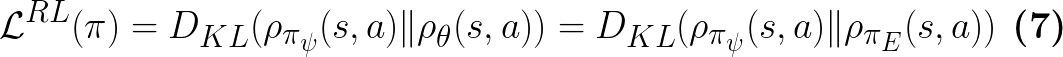
Eq.8 in paper
Similarly, when the discriminator is optimal,
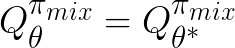 ,
as shown in Eq.8 in the paper:
,
as shown in Eq.8 in the paper:
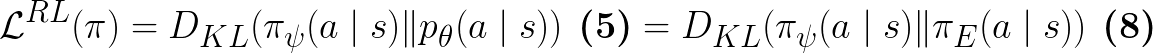
In comparison, the behavioral cloning (BC) objective is:
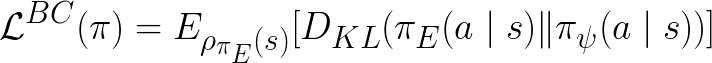
While it resembles our policy objective, the importance difference is that ours is under
 , state distribution of the combined cumulative experience of the robot and the expert,
which is a much wider distribution than the expert state distribution
, state distribution of the combined cumulative experience of the robot and the expert,
which is a much wider distribution than the expert state distribution
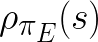 in the BC case.
in the BC case.
Lemma 1: Policy Improvement under Soft Q-functioned IRL
Here, we want to prove that by optimizing the policy using Eq.4, we are improving the policy each iteration.
Proof. Suppose  is the new policy we acquire from updating the policy using Eq.4:
is the new policy we acquire from updating the policy using Eq.4:
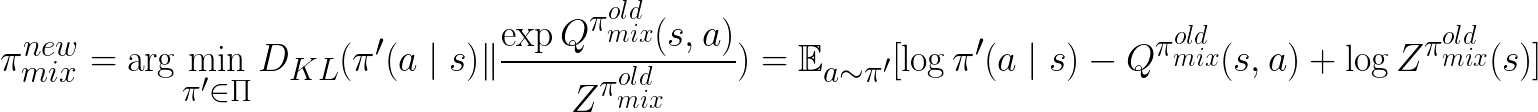
where 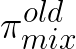 is the old policy before each update during training.
is the old policy before each update during training.
Since we can always choose
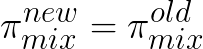 ,
we have:
,
we have: 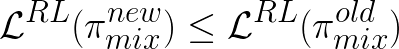 .
In other words:
.
In other words:
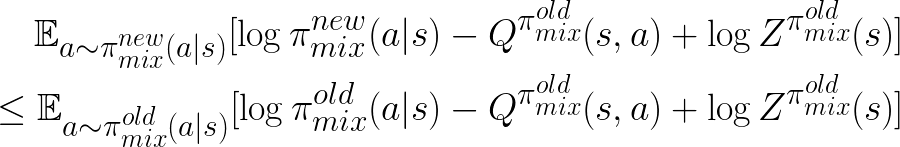
Since 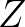 only depends on the states,
we have:
only depends on the states,
we have:
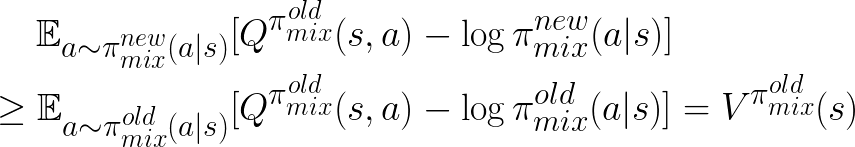
where 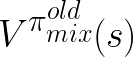 is the soft value function for the policy before the training update.
Hence, the Q-function under the new mixture policy is greater or equal to the old one.
is the soft value function for the policy before the training update.
Hence, the Q-function under the new mixture policy is greater or equal to the old one.
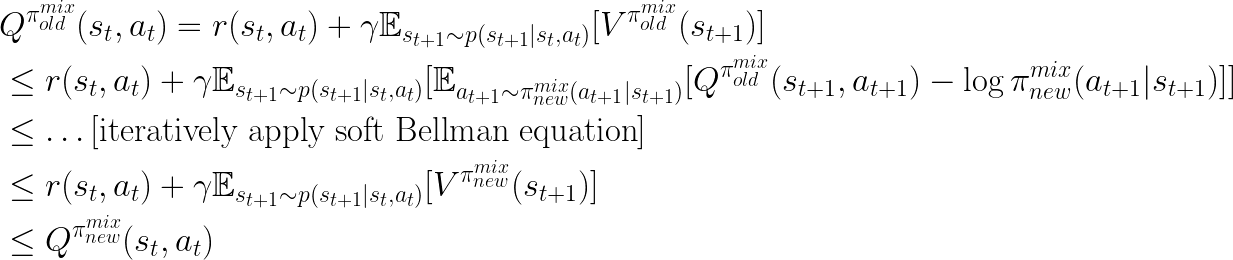
Since the new robot policy 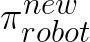 is the only variable component in
is the only variable component in
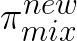 (with the expert policy
(with the expert policy
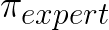 being fixed),
by optimizing this objective, we are able to get an improved performance on
being fixed),
by optimizing this objective, we are able to get an improved performance on
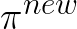 .
.
Acknowledgment
This work is supported by NSF Grant CMMI-1734557. We thank Prof. Shuran Song for UR5 Hardware Support. We also thank Google for the UR5 robot, Zhenjia Xu for UR5 Hardware Setup, and everyone at Columbia RoboVision and Columbia Robotics Lab for logistical assistance.